Samstag, 26. März 2016

Raw Materials and Resources - Part 9

Ressourcen und Gesellschaft – Teil 9

Die Verfügbarkeit und der Verbrauch von natürlichen Ressourcen haben unzweifelhaft Auswirkungen auf die Entwicklung biologischer und gesellschaftlicher Systeme. Es gibt zahlreiche heuristische Modelle, die uns helfen diese Entwicklungen besser zu verstehen. Diese Modelle wirken dabei als Brücke zwischen dem reduktionistischen Charakter empirischer Beobachtungen und formalen Theorien. Sie erlauben uns, die Komplexität der Makroevolution zu vereinfachen und dabei trotzdem die Evolution biologischer und gesellschaftlicher Systeme (hoffentlich) angemessen widerzuspiegeln (Quelle). Einige dieser Modelle möchte ich hier vorstellen.



Daisyworld

In der Computersimulation Daisyworld gibt es auf einem simulierten erdähnlichen Planeten nur zwei Arten von Lebewesen: schwarze und weiße Gänseblümchen. Weiße Gänseblümchen reflektieren Licht und schwarze Gänseblümchen absorbieren Licht. Beide Arten wachsen gleich schnell, jedoch reflektieren schwarze Gänseblümchen weniger Sonnenlicht (25%) als weiße (75%) und die kahle Erde (50%). Ein Planet mit einem Übergewicht an weißen Gänseblümchen ist durch die größere Reflektion des Lichtes kühler als einer mit mehr schwarzen. Wird die Simulation ohne die Gänseblümchen durchlaufen, steigt der Temperaturverlauf synchron zur Strahlungsleistung der Sonne. Mit Gänseblümchen gibt es zu Beginn der Simulation verstärkte Erwärmung und zum Ende verstärkte Kühlung, was zu einer nahezu konstanten Gleichgewichtstemperatur während des größten Teils der Simulation führt. Auf diese Weise verändern die Gänseblümchen das Klima derart, dass die Bedingungen für sie lebensfreundlicher werden.

Spätere Erweiterungen des Daisyworldmodells schlossen Kaninchen, Füchse und andere Arten mit ein, welche Absorptionsraten zwischen den schwarzen und weißen Daisys haben. Eines der überraschenderen Ergebnisse dieser Simulationen war, dass die selbstregulierenden Kräfte des gesamten Planeten mit der Anzahl der Arten stiegen. Diese Beobachtung unterstützte die Ansicht, dass Biodiversität wertvoll ist, und löste die moderne Biodiversitätsdebatte aus.
Das stark vereinfachende Daisyworldmodell zog natürlich auch Kritik auf sich. Die Simulation weist kaum Ähnlichkeit mit der Erde auf; das System benötigt eine konstante Todesrate, um im Gleichgewicht zu bleiben, und das Modell verwischt die Unterschiede zwischen Phänomenen auf der Ebene der Arten und jener der Individuen. Jedoch zeigt Daisyworld unbestreitbar, dass ein biologisch reguliertes Gleichgewicht keine teleologische Erklärung benötigt. (Quellen: Wikipedia und B. Alicea, R. Gordon: „Toy models for macroevolutionary patterns and trends“, Biosystems 123 (2014) 54-66)

Die Daisyworld-Simulation ist auf der Webseite gingerbooth.com online verfügbar und kann dort getestet werden (siehe Abbildung).


Abbildung: Screenshot der Simulation DaisyBall von der Webseite gingerbooth.com.



Lotka-Volterra-Regeln

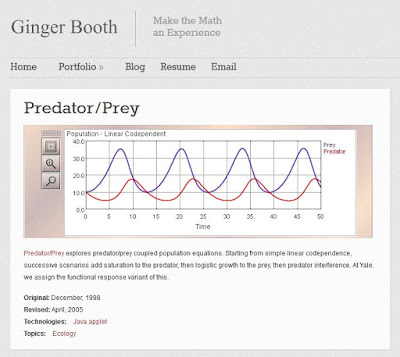
Die Lotka-Volterra-Regeln beschreiben die zahlenmäßige Entwicklung einer Raubtier- und einer Beutetierpopulation über große Zeiträume. Die Regeln gelten unter der Voraussetzung, dass nur zwischen diesen beiden Arten eine Räuber-Beute-Beziehung besteht und die sonstigen biotischen und abiotischen Umweltfaktoren konstant oder zu vernachlässigen sind. Die Regeln lauten folgendermaßen:
  • Erste Lotka-Volterra-Regel (Periodische Populationsschwankung): Die Populationsgrößen von Räuber und Beute schwanken periodisch. Dabei folgen die Schwankungen der Räuberpopulation phasenverzögert denen der Beutepopulation. Die Länge der Perioden hängt von den Anfangsbedingungen und von den Wachstumsraten der Populationen ab.
  • Zweite Lotka-Volterra-Regel (Konstanz der Mittelwerte): Die über genügend lange Zeiträume gemittelten Größen (Mittelwert) der Räuber- bzw. Beutepopulation sind konstant. Die Größe der Mittelwerte hängt nur von den Wachstums- und Rückgangsraten der Populationen, nicht aber von den Anfangsbedingungen ab.
  • Dritte Lotka-Volterra-Regel (Störung der Mittelwerte): Werden Räuber- und Beutepopulation gleichermaßen proportional zu ihrer Größe dezimiert, so vergrößert sich kurzfristig der Mittelwert der Beutepopulation, während der Mittelwert der Räuberpopulation kurzfristig sinkt.


Abbildung: Grafische Darstellung der ersten Lotka-Volterra-Regel.

Als Lehrbuchbeispiel für die Lottka-Volterra-Regeln gelten die Fangaufzeichnungen der Hudson’s Bay Company, die über 90 Jahre lang geführt wurden. Danach schwankte der Eingang von Fellen von Luchsen (Räuber) und Schneeschuhhasen (Beute) mit einer Periode von 9,6 Jahren. Allerdings wird dieses Beispiel strenggenommen durch einen zweiten Räuber beeinflusst, nämlich die Jäger. (Quelle: Wikipedia)

Die Lotka-Volterra-Regeln sind nur unter Beachtung ihrer selten erfüllten Voraussetzungen anwendbar. Trotzdem werden sie in der Ökologie häufig angewendet, da man annimmt, dass sie auch bei komplexeren Nahrungsbeziehungen und schwankenden Umweltfaktoren brauchbare Abschätzungen liefern können. Die Grenzen dieses Modells zeigt C. A. S. Hall in dem Artikel “An assessment of several of the historically most influential theoretical models used in ecology and of the data provided in their support. “ Ecological Modelling, 43 (1988) 5-31.


Abbildung: Simulation einfacher Raubtier-Beute-Beziehungen unter http://gingerbooth.com/portfolio/predatorprey



Abbildung: Zur Simulation von komplexerer Raubtier-Beute-Beziehungen gibt es ein online-Tool unter http://www.learner.org



Tragik des Allgemeingutes

Der Begriff „Tragedy of the Commons“ bezeichnet im Englischen ein sozialwissenschaftliches und evolutionstheoretisches Modell, nach dem frei verfügbare aber begrenzte Ressourcen durch übermäßige Ausbeutung bedroht sind. Die fortwährende Übernutzung dieser Ressourcen führt zu deren Versiegen, was schließlich auch die Existenz der Nutzer selbst bedroht. Die wörtliche Übersetzung „Tragik der Allmende“ ist etwas ungewohnt, da der Begriff Allmende im Deutschen kaum noch verwendet wird. Beispiele für die problematische Nutzung Allen zu Verfügung stehender natürlicher Ressourcen sind:
  • die Überfischung der Weltmeere,
  • der Raubbau an tropischen Regenwäldern in Entwicklungsländern,
  • die Nutzung der Atmosphäre als Mülleimer für Luftschadstoffe.
Der Mikrobiologe und Ökologe Garrett Hardin erweiterte den Begriff 1968 in einem Beitrag für die Zeitschrift Science. Die Tragik des Allgemeingutes ist nach Hardin ein unvermeidliches Schicksal der Menschheit, für das es keine technologische Lösung gebe. Er erweiterte den Begriff zur Metapher für Übervölkerung und forderte unter anderem eine globale Geburtenkontrolle. (G. Hardin: The Tragedy of the Commons, Science 162 (1968) 1243-1248)

Peter Roopnarine entwickelte in jüngster Zeit mathematische Modelle zur Tragik des Allgemeingutes analog zu den ökologischen Modellen des Ressourcenverbrauchs (siehe oben). Tragödien spielen sich immer wieder in Ökosystemen ab, wo viele Spezies miteinander in Wechselwirkung stehen. Die Anzahl der vom Menschen ausgebeuteten Ressourcen wachsen stetig. Dadurch vernetzen die vom Menschen benötigten Ressourcen zunehmend zu ökosystemartigen Systemen. Die Wahrscheinlichkeit von systemweiten Tragödien steigt dabei immer weiter. Als Beispiel werden in dem Artikel die massiven Emissionen von Treibhausgasen durch die beiden bevölkerungsreichen Nationen China und USA genannt. Die globale Erwärmung bedroht alle küstennahen Völker durch das Ansteigen der Meeresspiegel, die Fischerei durch Erwärmen und Versauerung des Wassers und die Existenz von Korallenriffen und Inseln. (Peter Roopnarine: Ecology and the Tragedy of the Commons, Sustainability 5 (2013) 749-773)




Malthus-Katastrophe 

Thomas Robert Malthus (1766-1834) war ein britischer Ökonom. Er stellte die These auf, dass die Bevölkerungszahl exponentiell wächst, die Nahrungsmittelproduktion aber nur linear. Das sollte zur Folge haben, dass Nahrungsmittelangebot langfristig nicht mit dem Bevölkerungswachstum Schritt halten könne. Daher müssten die Nahrungsmittelpreise steigen und die Reallöhne unter das Existenzminimum sinken. Malthus begründete damit Armut, Hunger, Krankheit, Slumbildung und die daraus sich ergebenden sozialen Unruhen in den englischen Großstädten seiner Zeit. Malthus hielt das für ein Naturgesetz. Im weiteren Verlauf erwartete er, dass die fortschreitende Verelendung der Bevölkerung durch Krankheit und Seuchen die Bevölkerung wieder reduziere. Danach sollte der Zyklus von neuem beginnen. Malthus unterschätzte die Geschwindigkeit des technischen Fortschritts, die vor allem in der Landwirtschaft die Produktivität erheblich erhöhte. (Quelle: Wikipedia)



Abbildung: Malthus-Katastrophe



Die Grenzen des Wachstums

An dieser Stelle sollte auch die Studie „Die Grenzen des Wachstums“ erwähnt werden. Die 1972 veröffentlichte Studie wurde im Auftrag des Club of Rome erstellt. Die Studie zeigt, dass das aktuelle individuelle lokale Handeln Aller globale Auswirkungen hat, die jedoch nicht dem Zeithorizont und Handlungsraum der Einzelnen entsprechen. Dazu wurde eine Systemanalyse und Computersimulationen verschiedener Szenarien durchgeführt. Das benutzte Weltmodell diente der Untersuchung von fünf Tendenzen mit globaler Wirkung:
  • Industrialisierung,
  • Bevölkerungswachstum,
  • Unterernährung,
  • Ausbeutung von Rohstoffreserven und
  • Zerstörung von Lebensraum.
So wurden Szenarien mit unterschiedlich hoch angesetzten Rohstoffvorräten der Erde berechnet, oder eine unterschiedliche Effizienz von landwirtschaftlicher Produktion, Geburtenkontrolle oder Umweltschutz angesetzt.(Quelle: Wikipedia) Die zentralen Schlussfolgerungen des Berichtes waren: „Wenn die gegenwärtige Zunahme der Weltbevölkerung, der Industrialisierung, der Umweltverschmutzung, der Nahrungsmittelproduktion und der Ausbeutung von natürlichen Rohstoffen unverändert anhält, werden die absoluten Wachstumsgrenzen auf der Erde im Laufe der nächsten hundert Jahre erreicht. Mit großer Wahrscheinlichkeit führt das zu einem ziemlich raschen und nicht aufhaltbaren Absinken der Bevölkerungszahl und der industriellen Kapazität“. (D. Meadows, D. Meadows, E. Zahn, P. Milling: Die Grenzen des Wachstums. Bericht des Club of Rome zur Lage der Menschheit, Deutsche Verlagsanstalt, Stuttgart 1972, S. 17)

Die Veröffentlichung des Berichtes führte zu äußerst kontroversen Diskussionen. Einige kritisierten ein Ausblenden des technischen Fortschritts in einer reinen Extrapolation von gegenwärtigen Trends. Andere bemängelten eine uneinheitliche Verwendung von Wachstumsfaktoren: Bevölkerung, Kapital und Umweltverschmutzung wuchsen im Modell exponentiell, während bei Technologien zu Ressourcennutzung und zum Umweltschutz nur ein lineares Wachstum angenommen wurde. In dieser Hinsicht erinnert die Studie an das Modell von Malthus (siehe oben). (Quelle und weitere Informationen: Wikipedia)

Links:

Eingestellt von um Keine Kommentare:
Labels: , ,

Mittwoch, 23. März 2016

Raw Materials and Resources - Excursus B

Fraktale –Exkurs B

Der Begriff Fraktal wurde von Benoît B. Mandelbrot geprägt. Er ist vom lateinischen Wort fractus „gebrochen“ abgeleitet. Ein Fraktal ist ein natürliches Phänomen oder ein Satz mathematischer Gleichungen, die ein sich wiederholendes Muster auf jeder Skale haben. Wenn die Replikation auf jeder Skale genau gleich ist, spricht man von einem selbstähnlichen Muster. Fraktale unterscheiden sich in der Art in der sie skalieren. Beim Verdoppeln der Kantenlänge eines Polygons vergrößert sich die Fläche des Polygons um den Faktor 4 (= 22). Beim Verdoppeln des Radius einer Kugel vergrößert sich das Volumen der Kugel um den Faktor 8 (=23). Wenn jedoch bei einem Fraktal alle eindimensionalen Längen verdoppelt werden, so skaliert der Rauminhalt des Fraktals nicht unbedingt geradzahlig. Dieser Exponent wird als die fraktale Dimension bezeichnet. (Quelle)

Für ein fraktales System reicht ein Exponent zur Beschreibung aus. Bei einem multifraktalen System reicht ein Exponent zur Beschreibung nicht aus, sondern es wird ein kontinuierliches Spektrum von Exponenten benötigt. Multifraktale Systeme treten in der Natur häufig auf. Sie werden zur Beschreibung der verschiedensten Erscheinungen genutzt, so z.B. für Turbulenzen in der Fluiddynamik, Internetverkehr, Finanzmärkte, Bilderzeugung, Meteorologie oder Geophysik. (Quelle)

Abbildung: Mandelbrot-Fraktal erzeugt mit dem Mandelbrot Set Generator.
Eingestellt von um Keine Kommentare:
Labels:

Samstag, 19. März 2016

Raw Materials and Resources - Excursus A

Wahrscheinlichkeitsverteilungen

Im letzten Post wurden verschiedene Verteilungsfunktionen besprochen. Zur Klärung der Begriffe an dieser Stelle einige Erklärungen und bei Interesse weiterführende Links.

Die Normalverteilung (auch Gaußverteilung oder Glockenkurve) entsteht durch die Überlagerung einer großen Zahl von unabhängigen Einflüssen. Zufällige Abweichungen treten in vielen wissenschaftlichen Disziplinen und Lebensbereichen auf. So liegen z.B. bei folgenden Vorgängen Normalverteilungen vor:
  • zufällige Messfehler,
  • Abweichungen vom Sollmaß bei der Fertigung von Werkstücken,
  • bei der Brownschen Molekularbewegung,
  • Milchproduktion von Kühen,
  • Verteilung der Intelligenz bei Menschen.
Die Normalverteilung ist durch folgende Formel definiert:
 

Die dabei entstehende typische Glockenkurve (siehe Abbildung) wird durch zwei Parameter charakterisiert: den arithmetischen Mittelwert μ der Standardabweichung (Varianz) σ. Datensätze werden daher häufig mit μ±σ angegeben. (Quellen: Wikipedia, Mathepedia)
In der Natur zeigen allerdings viele Messdaten mehr oder weniger schiefe Verteilungen. Schiefe Verteilungen treten vor allem auf, wenn die Durchschnittswerte niedrig und die Standardabweichungen groß sind. Beispiele für solche schiefen Verteilungen sind die Häufigkeit von Species, die Länge von Latenzzeiten von Infektionskrankheiten und die Verteilung von Mineralen in der Erdkruste. Solche schiefen Verteilungen können häufig mit einer Log-Normalverteilung beschrieben werden. (Quelle)

Die Logarithmische Normalverteilung (abgekürzt: Log-Normalverteilung, engl.: log-normal distribution) ist eine kontinuierliche Wahrscheinlichkeitsverteilung. Sie beschreibt die Verteilung einer Zufallsvariablen x, wenn ln(x) normalverteilt ist.
 



Logarithmische Normalverteilungen treten z.B. auf bei:
  • Durchmesser von Bäumen
  • Breite von Hanfbastfasern
  • Durchmesser von Bakterien
  • Körpergröße des Menschen
  • Verteilung der Galaxien
  • Wachstumsgröße von Kristallen
Wie kommt es zu einer Log-Normalverteilung?

Normalverteilung und logarithmische Normalverteilung basieren auf einer Vielzahl von Kräften die unabhängig voneinander einwirken. Ein wichtiger Unterschied ist, dass diese Effekte additiv oder multiplikativ sein können. Die additive Anhäufung von Effekten führt zur Normalverteilung, die multiplikative zur Log-Normalverteilung. (Quelle)
Eine multiplikative Verknüpfung kann durch logarithmieren in eine additive Verknüpfung überführt werden: Die Logarithmierung des Produktes a.b führt gemäß Logarithmengesetzen zu ln(a.b) = ln(a) + ln(b).
Additive Effekte werden in der Mathematik durch eine arithmetische Folge (an=a0+n.d) oder auch dem arithmetischen Mittelwert beschrieben. Multiplikative Effekte werden durch eine geometrische Folge (an=a0.qn) oder den geometrischen Mittelwert beschrieben. Diese Zusammenhänge haben Gebelein und Heite in ihrem Artikel „Über die Unsymmetrie biologischer Häufigkeitsverteilungen“ (Klinische Wochenschrift 28 (1950) 41-45) sehr schön dargestellt. (siehe Abbildung). Bei einer grafischen Darstellung der arithmetischen Reihe liegen konstante Abstände zwischen den Gliedern der Reihe vor: d=x2-x1=x3-x2=…= konstant. Dieser Sachverhalt ist in der nachfolgenden Abbildung (links) durch Aneinanderreihen kongruenter Dreiecke zwischen parallelen Geraden visualisiert. Im Unterschied dazu ist bei einer geometrischen Reihe der Quotient zwischen den Gliedern der Reihe konstant:
Das wird in der unten stehenden Abbildung (rechts) durch Aneinanderfügen ähnlicher Dreiecke zwischen zwei sich schneidenden Geraden dargestellt. Für beide Folgen wird die Summe als Funktion dargestellt (Abbildung oben). Die Ableitung dieser beiden Funktionen führt zur Normalverteilung (unten links) bzw. zur logarithmischen Normalverteilung (unten rechts).


Abbildung: Zusammenhang zwischen arithmetischer Folge und Normalverteilung (links) und Zusammenhang zwischen geometrischer Folge und Logarithmischer Normalverteilung (rechts) nach Gebelein und Heite.

Links:



    Die Pareto-Verteilung wird durch ein Potenzgesetz definiert:



    Die Verteilung ist nach Vilfredo Pareto benannt. Er verwendete diese 1897 zur Beschreibung der Einkommensverhältnisse in Italien. Ein großer Anteil der Bevölkerung verdient wenig. Je höher die Einkommen werden, desto weniger Personen erhalten diese. Pareto-Verteilungen finden sich charakteristischerweise dann, wenn sich zufällige, positive Werte über mehrere Größenordnungen erstrecken und durch das Einwirken vieler unabhängiger Faktoren zustande kommen. Verteilungen mit ähnlichen Eigenschaften sind das Zipfsche-Gesetz und das Benfordsche Gesetz. (Quelle Wikipedia)

    Mit der Pareto-Verteilung kann man folgende Sachverhalte beschreiben:
    • Verteilung des Einkommens
    • Einwohnerzahlen von Städten
    • Schadenshöhen in der Versicherungsmathematik
    In Wirtschaft und Industrie wird häufig die 80/20-Regel („Pareto-Prinzip“) verwendet. Diese ist von der Pareto-Verteilung abgeleitet. Diese Regel besagt, dass 80 % der Ergebnisse mit 20 % des Gesamtaufwandes erreicht werden. Die verbleibenden 20 % der Ergebnisse benötigen mit 80 % Aufwand die meiste Arbeit. Im Projekt- und Zeitmanagement verwendet man diese Regel, um wichtige Arbeitspakete zu erkennen und schnelle Fortschritte bei relativ guten Ergebnissen zu erzielen. Beispiele für die Anwendung dieser Regel sind:
    • 80 % des Umsatzes von Firmen werden meist mit 20 % der Produkte erzielt.
    • 80 % der Stadtbewohner eines Landes leben in 20 % der Städte.
    • 80 % der Anrufe führt man im Allgemeinen mit 20 % seiner gespeicherten Kontakte.


    Logarithmische Darstellungen


    In Natur- und Ingenieurwissenschaften werden oft logarithmische Darstellungen verwendet. Der Log-Log- Plot ist eine zweidimensionale Darstellung von numerischen Daten mit logarithmischen Skalen auf der x- und y-Achse. Potenzfunktionen des Typs y = a xbx erscheinen in einer solchen Darstellung als gerade Linie. Diese Darstellung ist sehr nützlich, da daraus in einfacher Weise die Parameter des Potenzgesetzes bestimmt werden können: Die Steigung der Geraden ergibt den Parameter b der Potenzfunktion, der Schnittpunkt mit der y-Achse entspricht dem Logarithmus von a. Außerdem bietet eine solche Darstellungsweise weitere Vorteile, denn die lineare Regression hat am PC eine größere Genauigkeit als andere Regressionen. Dies hängt mit der verfügbaren Speichergröße von Fließkommazahlen am PC zusammen.

    Im Post „Verteilung von Ressourcen“ haben wir die Log-Log-Darstellung bereits genutzt, um den Unterschied zwischen der Pareto-Verteilung und der Log-Normalverteilung deutlich zu machen (siehe Abbildung).


    Abbildung: Log-Log-Darstellung der Lagerstättengröße über der Wahrscheinlichkeit für Mineralvorkommen.
    Links:



      Mein Dank gilt Marcus Herbig für Hinweise und Korrekturen in diesem Abschnitt.
      Eingestellt von um Keine Kommentare:
      Labels: , ,

      Samstag, 12. März 2016

      Raw Materials and Resources - Part 8

      Mandelbrot und die Verteilung der Rohstoffe

      Im letzten Post wurde Benoit Mandelbrot erwähnt. Zur genaueren Kenntnis habe ich mir das genannte Buch besorgt (Quellen am Ende des Posts). In dem Werk wird umfassend das Auftreten fraktaler Verteilungen in Natur, Kosmos und Gesellschaft analysiert. An einer Stelle geht er auch kurz auf die räumliche Verteilung von Öl und anderen Rohstoffvorkommen ein. In dem Kapitel geht es hauptsächlich um das Relief der Erdoberfläche und die Gestalt von Küstenlinien. Weiter geht es mit der Gestalt von zerbrochenen Steinen.
      Mandelbrot schlussfolgert, dass jede mit dem Relief zusammenhängende Größe einer hyperbolischen Wahrscheinlichkeitsverteilung folgt (Pareto-Verteilung). Weiter heißt es: „Die Untersuchung der Küstenlinien, die auf ein skaleninvariantes Relief hinwies, war von Mandelbrot (1962n) eingeleitet worden. Dort wurden auch die Verteilungen im Zusammenhang mit Öl- und anderen Rohstoffvorkommen als hyperbolisch erkannt. Dieses Ergebnis widerspricht der vorherrschenden Meinung, derartige Quantitäten seien logarithmisch normalverteilt. Der Unterschied ist extrem signifikant. Unter dem hyperbolischen Gesetz sind die Reserven viel größer als unter der logarithmischen Normalverteilung. Mein Schluss fand 1962 nicht viel Gehör, aber ich werde es wieder versuchen.“
      Die angegebene Quelle “1962n” ist B. B. Mandelbrot: „Statistics of natural resources and the law of Pareto“ IBM Research note NC-146, 29. Juni 1962 (unveröff.).” Vermutlich fand diese Erkenntnis 1962 keine Beachtung, weil es sich um eine interne IBM-Veröffentlichung handelte.

      Abschließend noch die Quellenangaben zu dem genannten Buch:
      • B. B. Mandelbrot „The fractal geometry of nature – Updated and Augmented“ W. H. Freeman and Company, New York 1983, Seite 263.
      • Eine deutschsprachige Ausgabe ist z.B: B. B. Mandelbrot: „Die fraktale Geometrie der Natur“Birkhäuser Verlag, Basel 1991, Seite 279-280. Die entsprechende Textstelle findet man auch bei Google Books.
      Eingestellt von um Keine Kommentare:
      Labels: ,

      Samstag, 5. März 2016

      Raw Materials and Resources - Part 7

      Verteilung von Ressourcen

      Sehr hilfreich wären Informationen darüber wo, wie viele und vor allem wie große noch unentdeckte Lagerstätten von Mineralien zu finden sein könnten. Kann man mit Hilfe statistischer Methoden, auf der Grundlage der bereits bekannten Lagerstätten, Aussagen über die Verteilung und die Reichweite natürlicher Ressourcen treffen? Leider erfahren wir aus einem Lehrbuch der Lagerstättenkunde, dass solche Vorhersagen nicht möglich sind: „Man kann natürlich argumentieren, dass Lagerstätten durch physikalisch-chemisch und chemisch beschreibbare Prozesse entstehen und daher Gehaltsverteilungen auch mathematisch beschreibbar sein müssen. Es spielen jedoch so viele Parameter, die sich von Ort zu Ort ändern können, mit hinein, dass eine generelle Aussage über Häufigkeitsverteilungen bei Lagerstätten nicht gemacht werden kann.“ (Quelle: F.-W. Wellmer: Rechnen für Lagerstättenkundler und Rohstoffwirtschaftler, Teil 2: Lagerstättenstatistik, Explorationsstatistik einschließlich geostatischer Methoden“ Verlag Ellen Pilger, Clausthal-Zellerfeld, 1989, Seite 40) Eventuell bezieht sich diese Aussage im engeren Sinne nur auf die Häufigkeitsverteilung innerhalb einer einzelnen Lagerstätte. Das ist mir beim Lesen nicht ganz klar geworden. Viel interessanter sind Häufigkeitsverteilungen von Minerallagerstätten in großen Regionen oder ganzen Kontinenten.
      Die aktuelle Fachliteratur liefert durchaus Aussagen zur Verteilung natürlicher Ressourcen. So nutzt F.P. Agterberg vom Geological Survey of Canada z.B. multifraktale Modellierung zum Abschätzen der Größen und Gehalte von großen und supergroßen Metalllagerstätten (F. P. Agterberg: „Multifractal Modeling of the Sizes and Grades of Giant and Supergiant Deposits” International Geology Review 37 (1995) 1-8). Dabei weist er auf den Unterschied zwischen fraktaler und multifraktaler Modellierung hin: Ein fraktales Modell ist für einen Satz von Objekten gültig. Für eine räumliche Analyse können begrenzte Objekte mit Hilfe von binären Variablen modelliert werden. Das bedeutet, das Objekt ist an einem bestimmten Punkt im Raum anwesend oder abwesend (Eins oder Null als binäre Variable). Nur ein Satz von Objekten derselben Art mit unterschiedlicher Gestalt und Größe kann mit fraktaler Modellierung beschrieben werden.
      Für Messgrößen benötigt man dagegen ein multifraktales Modell. Das betrifft z. B. räumlich verteilte unterschiedlich große Metallkonzentrationen. Mit Hilfe der multifraktalen Modellierung von Metalllagerstätten konnte Agterberg zeigen, dass die Häufigkeitsverteilung supergroßer Lagerstätten einem Potenzgesetz, bzw. der Pareto-Verteilung gehorcht. Als Alternative wird in der Fachliteratur häufig eine logarithmische Normalverteilung (Log-Normalverteilung) zur Beschreibung der Häufigkeitsverteilung von Lagerstätten angenommen. Der Unterschied zwischen den beiden Häufigkeitsverteilungen wird aus nachfolgender Abbildung deutlich. Die Pareto-Verteilung (rote Linie) ergibt bei einer Darstellung in einer doppeltlogarithmischen Grafik eine Gerade. Im Gegensatz dazu liefert die Log-Normalverteilung eine gebogene Linie (blau).



      Abbildung: Die Log-Normalverteilung im Vergleich mit der Pareto-Verteilung bei doppeltlogarithmischer Darstellung nach Agterberg 1995. 

      Im linken Bereich der Grafik ist die Linie der Pareto-Verteilung deutlich über der Linie der log-Normalverteilung. Das bedeutet in der Praxis, dass es viel mehr große Lagerstätten geben sollte, als man bisher annahm!
      Agterberg weist darauf hin, dass die logarithmische Normalverteilung zur Beschreibung der Größen und Gehalte der meisten Lagerstätten ein gutes Modell darstellt. Wenn man jedoch die größten Lagerstätten mit einbezieht, sollte die Pareto-Verteilung gültig sein.
      Mandelbrot wies bereits 1983 in seinem Buch über die fraktale Geometrie der Natur darauf hin, dass Öl und andere natürliche Ressourcen einer Pareto-Verteilung folgen sollten (B.B. Mandelbrot „The fractal geometry of nature“ Freeman, New York 1983, Seite 263).
      Empirische Daten deuten darauf hin, dass die Dichte von Lagerstätten dem Potenzgesetz gehorcht. Dazu formulierte Donald A. Singer vom US Geological Survey folgende einfache Beziehung: Dichte [d/km2] = S.Aβ. Dabei ist A das Gebiet in dem aus geologischen Gründen unentdeckte Mineralvorkommen auftreten können („permissive area“). Der Exponent β ist für die in der zitierten Arbeit untersuchten Gebiete ungefähr 0,6. Der Faktor S variiert mit der Art des Mineralvorkommens. (Quelle: D. A. Singer: „Mineral Deposit Densities for Estimating Mineral Resources”, Math. Geosci. 40 (2008) 33–46) In der gleichen Arbeit wird erklärt, dass die log-Normalverteilung für die meisten Minerallagerstätten ein geeignetes Modell zur Beschreibung des beobachteten Abbauvolumens ist.
      Log-Normale Verteilungen entstehen häufig als Produkt aus vielen unabhängigen kleinen Faktoren. Viele Gesetze der Chemie und Physik wirken multiplikativ bei der der Bildung und Erhaltung von Erzlagerstätten. Zu diesen Faktoren zählen z.B. der Transport von Metallionen in hydrothermalen Systemen und die Geschwindigkeit von einfachen chemischen Reaktionen, die wiederum vom Produkt der Konzentrationen der beteiligten chemischen Spezies abhängt. Diese Prozesse sind größenunabhängig und nützlich zum Verständnis der Beziehungen zwischen Lagerstättengröße und der Anzahl der der Lagerstätten. (Quelle)
      In einer neueren Arbeit zeigte Singer allerdings, dass die logarithmische Normalverteilung für viele gut untersuchte Mineralvorkommen eine schlechte Näherung darstellt (D. A. Singer: “The lognormal distribution of metal resources in mineral deposits”, Ore Geology Reviews 55 (2013) 80–86).
      Der United States Geological Survey verwendet ein dreistufiges Verfahren, um unbekannte Mineralvorkommen zu beurteilen. Dieses Verfahren ist in der nachstehenden Abbildung skizziert. Zuerst werden geologische Daten genutzt, um Gebiete zu identifizieren, in denen unentdeckte Mineralvorkommen auftreten können (in der Abbildung links oben beginnend). Im zweiten Schritt wird die Zahl der bisher nicht entdeckten Mineralvorkommen abgeschätzt. Im dritten Schritt wird die Menge der in diesen Mineralvorkommen zu erwartenden Ressourcen mit statistischen Methoden geschätzt. Die quantitative Ressourcenanalyse wird mit ökonomischen und politischen Analysen kombiniert und weiter verarbeitet (in der Mitte der Abbildung). Auf der rechten Seite sind dann die Ergebnisse dieser Analyse dargestellt. Dabei ist nicht nur die potenzielle Bereitstellung von Mineralien durch Bergbau von Interesse, sondern es werden weitere Faktoren berücksichtigt. Dazu gehören Umweltaspekte, Landverbrauch durch Bergbau und ökonomische Aspekte (rechte Seite der Abbildung).


      Abbildung: Das dreistufige Verfahren des US Geological Survey zur quantitativen Beurteilung von Mineralvorkommen. (Quelle der Abbildung: USGS)


      Fazit: Mit Hilfe statistischer Methoden lassen sich Aussagen über die Verteilung und die Reichweite natürlicher Ressourcen treffen. Außerdem können statistische Methoden beim Auffinden und bei der Erschließung natürlicher Ressourcen helfen. Allerdings weisen die widersprüchlichen Aussagen zur Art der statistischen Zusammenhänge darauf hin, dass es hier noch deutlichen Forschungsbedarf gibt. Wohin die Entwicklung zur Beurteilung unbekannter Mineralvorkommen wahrscheinlich geht, zeigt das dreistufige Verfahren des United States Geological Survey. 

      Weitere Links:
      Diese Links stellen nur eine kleine Auswahl der verfügbaren Literatur dar. Bitte haben Sie Verständnis, dass ich hier keine umfassende Literatursammlung zur Quantitativen Beurteilung von Mineralvorkommen wiedergebe.
      Falls Sie noch wichtige Hinweise, Ideen oder Links zum Thema haben, schreiben Sie doch einfach einen Kommentar.


      Hoch innovativ und sexy - die Suche nach Rohstoffen! Schauen Sie sich dieses Video an:
      Ohne die enthaltenen High-Tech-Rohstoffe wären unsere Smartphones immer noch Science Fiction. Wenn wir in Europa die digitale Revolution anführen wollen, brauchen wir Innovationen, Ressourceneffizienz, Recycling und eine nachhaltige Versorgung mit Rohstoffen.

      Eingestellt von um Keine Kommentare:
      Labels: , ,
      Abonnieren Posts (Atom)